Рассчитать балку на прогиб

Расчет деревянных балок перекрытия – Калькулятор онлайн

Онлайн-калькулятор для расчета балки на прогиб/изгиб и прочность. Расчет деревянных балок перекрытия на прогиб. Подбор сечения балки.

Балка – это элемент строительных несущих конструкций, который широко используется для возведения межэтажных перекрытий. Перекрытия, в свою очередь, предназначены для разделения по высоте смежных помещений, а также принятия статических и динамических нагрузок от находящихся на нем предметов интерьера, оборудования, людей и т.д.

В большинстве случаев, для частного домостроения используются деревянные балки из цельного бруса, отесанного бревна, клееных досок или шпона. Эти материалы, при правильном подборе параметров, способны обеспечить необходимую прочность и жесткость основания, что является залогом долговечности постройки.

Мы предлагаем вам выполнить онлайн расчет балки перекрытия на прочность и изгиб, подобрать её сечение и определить шаг между балками. Также вы получите набор персональных чертежей и 3D-модель для лучшего восприятия возводимой конструкции. Программа учитывает СНиП II-25-80 (СП 64.13330.2011) и другие справочные источники.

Точный и грамотный расчет деревянных балок в сервисе KALK.PRO, позволяет узнать все необходимые параметры для сооружения крепкого перекрытия. Все вычисления бесплатны, есть возможность сохранения рассчитанных данных в формате PDF, плюс доступны схемы и 3D-модель.

Инструкция к калькулятору

Наш сервис предоставляет на выбор два вида расчета однопролетных балок перекрытия. В первом случае, вам предлагается рассчитать сечение балки при известном шаге между ними, во втором случае, вы можете узнать рекомендуемое значение шага между балками при выбранных характеристиках сечения. Разберем работу калькулятора на примере, когда ваша задача заключается в нахождении сечения балки.

Для расчета вам понадобится знать ряд обязательных начальных параметров. В первую очередь это характеристики самой балки:

• ширина сечения (толщина), мм;
• длина пролета балки (на изображении BLN), м;
• вид древесины (сосна, ель, лиственница…);
• класс древесины (1/К26, 2/К24, 3/К16);
• пропитка (есть, нет).

В случае, если вы не знаете толщину предполагаемой балки, в первом блоке следует выбрать пункт «Известно соотношение высоты сечения балки к её ширине — h/b» и указать значение 1,4. Эта наиболее оптимальная величина, которая получена эмпирическим методом и указывается во многих справочниках.

Затем нужно указать условия, в которых будет эксплуатироваться перекрытие:

• температурный режим ( 50 °C);
• влажностный режим;
• присутствуют постоянные повышенные нагрузки или нет.

После этого, сконфигурируйте конструкцию и заполните поля калькулятора:

• длина стены дома по внутренней стороне, м;
• шаг между балками, см;
• полная длина балки (на изображении BFL), м;
• нагрузка на балку, кг/м 2 ;
• предельный прогиб в долях пролета.

При необходимости впишите стоимость одного кубометра древесины, для того чтобы узнать общую стоимость всех пиломатериалов.

Также, обратим внимание, что обычно шаг балки не делают меньше 0,3 м, так как это нецелесообразно с экономической точки зрения и больше 1,2 м, так как возможен прогиб чернового пола со всеми вытекающими последствиями.

Когда вы нажмете кнопку «Рассчитать», сервис произведет расчет балки онлайн и выведет на экране рекомендуемые значения сечения подобранной балки.

Кроме того, в блоке «Результаты расчета» вы сможете узнать:

• параметры балки при расчете на прочность;
• параметры балки при расчете на прогиб;
• максимальный прогиб балки, см.

Квалифицированный расчет перекрытия по деревянным балкам — залог долговечности сооружения и безопасность для вашей семьи.

Расчет балок перекрытия

Самостоятельный расчет деревянной балки перекрытия – это долгое и нудное занятие, которое обязывает вас знать основы инженерных дисциплин и сопромата. Без определенных навыков и знаний, вручную подобрать материал, рассчитать необходимое сечение или шаг балки – не просто тяжело, а порой и невозможно. Тем не менее, мы попытаемся вам рассказать об основных характеристиках, которые нужны для вычислений и по какому алгоритму работает наш калькулятор.

Виды балок

В настоящее время, деревянные балки, используемые для изготовления перекрытий, можно разделить на два принципиально разных вида:

• цельные;
• клееные.

Исходя из названия становится понятно, что в первом случае, это будет цельный кусок древесины определенного типа сечения (чаще всего это брус на 2 или 4 канта), во втором случае, это клееная балка из досок или шпона LVL.

Несмотря на низкую стоимость, по ряду объективных причин, деревянные балки из цельной древесины в последнее время используются все реже. Качественные показатели этого материала значительно уступают клееному дереву: низкий модуль упругости способствует появлению больших прогибов в середине пролета (особенно это становится заметно при расстоянии между несущими стенами более 4 метров), при высыхании на балках появляются продольные трещины, которые приводят к уменьшению момента инерции прогиба, отсутствие пропитки подвергает древесину воздействиям вредителей и гниения.

Благодаря современным технологиям, клееные балки не имеют подобных недостатков. Их структура однородна и волокна ориентированы по всем направлениям – повышается общая прочность и модуль упругости материала, он получает защиту от растрескивания, а специальная пропитка обеспечивает повышенный уровень пожаробезопасности и устойчивости к влаге. Эти балки разрешено использовать при проемах в 6-9 м и можно рассматривать, как полноценный аналог железному перекрытию.

Расчет балки на прогиб — формулы, параметры и примеры решения

Расчет балки на прогиб нужно проводить практически для любой конструкции, чтобы проверить ее надежность и прочность. Под влиянием внешних, внутренних факторов, природных явлений балка подвержена деформации.

Балку сравнивают со стержнем, закрепленным на опорах. Чем больше опор, тем сложнее провести расчет самостоятельно. Основная нагрузка считается путем сложения сил, перпендикулярно направленных к сечению.

Данный расчет – основы сопромата, помогает определить наивысшую деформацию. Значения показателей должны входить в рамки допустимых величин.

Виды балок

При возведении зданий используется балки разных конфигураций, размеров, профиля, характера сечения. Их изготавливают из металла и дерева. Для любого вида используемого материала нужен индивидуальный расчёт изгиба.

Деревянные — их используют в основном при строительстве индивидуальных построек. Они применяются при возведении полов, потолков, несущих перекрытий. Дерево – капризный материал и подвержено деформации. Для определения максимального изгиба, существенны такие параметры: используемый профиль, размер, нагрузка, характер поперечного сечения.

Металлические — такие балки изготавливают из сплава металлов и сечение у них сложное. Поэтому особое внимание уделяется жесткости, а также прочности соединений. Балки из металла применяются в возведении многоэтажек, сооружений, требующих высокой прочности.

Прочность и жесткость балки

При проектировании следует учесть изгиб балок, чтобы конструкция была надежная, качественная, прочная и практичная.

На эти параметры влияют следующие факторы:

величина наружных нагрузок, их положение;

параметры, характер, нахождение поперечного сечения;

число опор, метод их закрепления.

Выделяют 2 метода исчисления: простой – применяется увеличительный коэффициент, и точный – дополнительно включает пограничные подсчеты.

Построение эпюр балки

Эпюра распределения величины нагрузки на объект:

Расчет на жесткость

В формуле обозначены:

M – max момент, возникающий в брусе;

W_n,min – момент сопротивления сечения (табличный показатель);

R_y – сопротивление на изгиб (расчётный показатель);

γ_c – показатель условий труда (табличный показатель).

Такой расчет не трудоемок, но для более верного значения требуется следующее:

рабочий план объекта;

определение характеристик балки, характер сечения;

определение max нагрузки, воздействующей на брус;

оценка точки max прогиба;

проверка прочности max изгибающего момента.

Расчет моментов инерции и сопротивления сечения

J – момент инерции сечения;

W – момент сопротивления.

Для определения данных параметров необходимо учитывать сечение по грани разреза. Если момент инерции возрастает, величина жесткости также возрастает.

Нахождение максимальной нагрузки и прогиба

Формула для вычисления:

q – нагрузка равномерно-распределенная;

E – гибкость (табличный показатель);

I – момент инерции сечения.

Нагрузки учитываются статические и периодические.

Расчет на прогиб и его особенности

Он необходим для всех перекрытий при высоких эксплуатационных нагрузках.

При применении соответствующих коэффициентов, придерживаются следующего:

балка, держащаяся на одной жесткой и одной шарнирной опоре, подвергающаяся воздействию сосредоточенной нагрузки;

балка, держащаяся на жесткой и шарнирной опоре, подвергающаяся воздействию распределенной нагрузки;

нагрузка консольного типа;

воздействие комплексной нагрузки.

Пример расчет балки на прогиб

Рассмотрим задачу из курса сопромата.

Дано: балка четырехугольного сечения 20 на 30 см; поперечная сила Q = 19 кН; изгибающий момент М = 28 кНм.

Необходимо рассчитать напряжение: нормальное и в пределе К, отдаленной на 11 см от оси, узнать прочность бруса из дерева, при [σ] = 10 МПа, [τ] = 3 МПа.

Чтобы узнать σ_(К), τ_(К), σ_max, τ_max определяем значение осевого момента инерции общего сечения I_Н.О., осевого момента сопротивления W_Н.О., статического момента отсеченного ряда и статического момента середины сечения S_max:

Из этого следует:

Определение прочности по нормальному напряжению:

Определение прочности по касательному напряжению:

При проектировании конструкций важно соблюдать все физико-механические вычисления на прочность. Удобно и качественно произвести расчеты может онлайн, что существенно сократит временные сроки.

Калькулятор выполняет подробный подсчет на основе формул, эпюр усилий, подбирает номер сечения металлической балки из прокатных профильных, двутавровых материалов, а также из металлических труб.

Формулы для расчета прогиба балки

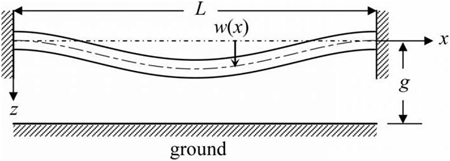
Балка является основным элементом несущей конструкции сооружения. При строительстве важно провести расчет прогиба балки. В реальном строительстве на данный элемент действует сила ветра, нагружение и вибрации. Однако при выполнении расчетов принято принимать во внимание только поперечную нагрузку или проведенную нагрузку, которая эквивалентна поперечной.

При расчете балка воспринимается как жесткозакрепленный стержень, который устанавливается на двух опорах. Если она устанавливается на трех и более опорах, расчет ее прогиба является более сложным, и провести его самостоятельно практически невозможно. Основное нагружение рассчитывается как сумма сил, которые действуют в направлении перпендикулярного сечения конструкции. Расчетная схема требуется для определения максимальной деформации, которая не должна быть выше предельных значений. Это позволит определить оптимальный материал необходимого размера, сечения, гибкости и других показателей.

Виды балок

Для строительства различных сооружений применяются балки из прочных и долговечных материалов. Такие конструкции могут отличаться по длине, форме и сечению. Чаще всего используются деревянные и металлические конструкции. Для расчетной схемы прогиба большое значение имеет материал элемента. Особенность расчета прогиба балки в данном случае будет зависеть от однородности и структуры ее материала.

Деревянные

Для постройки частных домов, дач и другого индивидуального строительства чаще всего используются деревянные балки. Деревянные конструкции, работающие на изгиб, могут использоваться для потолочных и напольных перекрытий.

Для расчета максимального прогиба следует учитывать:

1. Материал. Различные породы дерева обладают разным показателем прочности, твердости и гибкости.
2. Форма поперечного сечения и другие геометрические характеристики.
3. Различные виды нагрузки на материал.

Допустимый прогиб балки учитывает максимальный реальный прогиб, а также возможные дополнительные эксплуатационные нагрузки.

Стальные

Металлические балки отличаются сложным или даже составным сечением и чаще всего изготавливаются из нескольких видов металла. При расчете таких конструкций требуется учитывать не только их жесткость, но и прочность соединений.

Металлические конструкции изготавливаются путем соединения нескольких видов металлопроката, используя при этом такие виды соединений:

• электросварка;
• заклепки;
• болты, винты и другие виды резьбовых соединений.

Стальные балки чаще всего применяются для многоэтажных домов и других видов строительства, где требуется высокая прочность конструкции. В данном случае при использовании качественных соединений гарантируется равномерно распределенная нагрузка на балку.

Для проведения расчета балки на прогиб может помочь видео:

Прочность и жесткость балки

Чтобы обеспечить прочность, долговечность и безопасность конструкции, необходимо выполнять вычисление величины прогиба балок еще на этапе проектирования сооружения. Поэтому крайне важно знать максимальный прогиб балки, формула которого поможет составить заключение о вероятности применения определенной строительной конструкции.

Использование расчетной схемы жесткости позволяет определить максимальные изменения геометрия детали. Расчет конструкции по опытным формулам не всегда эффективен. Рекомендуется использовать дополнительные коэффициенты, позволяющие добавить необходимый запас прочности. Не оставлять дополнительный запас прочности – одна из основных ошибок строительства, которая приводит к невозможности эксплуатации здания или даже тяжелым последствиям.

Существует два основных метода расчета прочности и жесткости:

1. Простой. При использовании данного метода применяется увеличительный коэффициент.
2. Точный. Данный метод включает в себя использование не только коэффициентов для запаса прочности, но и дополнительные вычисления пограничного состояния.

Последний метод является наиболее точным и достоверным, ведь именно он помогает определить, какую именно нагрузку сможет выдержать балка.

Расчет на жесткость

Для расчета прочности балки на изгиб применяется формула:

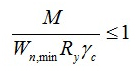
M – максимальный момент, который возникает в балке;

W_n,min – момент сопротивления сечения, который является табличной величиной или определяется отдельно для каждого вида профиля.

R_y является расчетным сопротивлением стали при изгибе. Зависит от вида стали.

γ_c представляет собой коэффициент условий работы, который является табличной величиной.

Расчет жесткости или величины прогиба балки является достаточно простым, поэтому расчеты может выполнить даже неопытный строитель. Однако для точного определения максимального прогиба необходимо выполнить следующие действия:

1. Составление расчетной схемы объекта.
2. Расчет размеров балки и ее сечения.
3. Вычисление максимальной нагрузки, которая воздействует на балку.
4. Определение точки приложения максимальной нагрузки.
5. Дополнительно балка может быть проверена на прочность по максимальному изгибающему моменту.
6. Вычисление значения жесткости или максимально прогиба балки.

Чтобы составить расчетную схему, потребуются такие данные:

• размеры балки, длину консолей и пролет между ними;
• размер и форму поперечного сечения;
• особенности нагрузки на конструкцию и точно ее приложения;
• материал и его свойства.

Если производится расчет двухопорной балки, то одна опора считается жесткой, а вторая – шарнирной.

Расчет моментов инерции и сопротивления сечения

Для выполнения расчетов жесткости потребуется значение момент инерции сечения (J) и момента сопротивления (W). Для расчета момента сопротивления сечения лучше всего воспользоваться формулой:

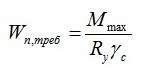
Важной характеристикой при определении момента инерции и сопротивления сечения является ориентация сечения в плоскости разреза. При увеличении момента инерции увеличивается и показатель жесткости.

Определение максимальной нагрузки и прогиба

Для точного определения прогиба балки, лучше всего применять данную формулу:

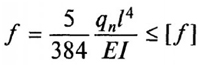
q является равномерно-распределенной нагрузкой;

E – модуль упругости, который является табличной величиной;

I – момент инерции сечения.

Чтобы рассчитать максимальную нагрузку, следует учитывать статические и периодические нагрузки. К примеру, если речь идет о двухэтажном сооружении, то на деревянную балку будет постоянно действовать нагрузка от ее веса, техники, людей.

Особенности расчета на прогиб

Расчет на прогиб проводится обязательно для любых перекрытий. Крайне важен точный расчет данного показателя при значительных внешних нагрузках. Сложные формулы в данном случае использовать необязательно. Если использовать соответствующие коэффициенты, то вычисления можно свести к простым схемам:

1. Стержень, который опирается на одну жесткую и одну шарнирную опору, и воспринимает сосредоточенную нагрузку.
2. Стержень, который опирается на жесткую и шарнирную опору, и при этом на него действует распределенное нагружение.
3. Варианты нагружения консольного стержня, который закреплен жестко.
4. Действие на конструкцию сложной нагрузки.

Применение этого метода вычисления прогиба позволяет не учитывать материал. Поэтому на расчеты не влияют значения его основных характеристик.

Пример подсчета прогиба

Чтобы понять процесс расчета жесткости балки и ее максимального прогиба, можно использовать простой пример проведения расчетов. Данный расчет проводится для балки с такими характеристиками:

• материал изготовления – древесина;
• плотность составляет 600 кг/м3;
• длина составляет 4 м;
• сечение материала составляет 150*200 мм;
• масса перекрывающих элементов составляет 60 кг/м²;
• максимальная нагрузка конструкции составляет 249 кг/м;
• упругость материала составляет 100 000 кгс/ м²;
• J равно 10 кг*м².

Для вычисления максимальной допустимой нагрузки учитывается вес балки, перекрытий и опор. Рекомендуется также учесть вес мебели, приборов, отделки, людей и других тяжелых вещей, который также будут оказывать воздействие на конструкцию. Для расчета потребуются такие данные:

• вес одного метра балки;
• вес м2 перекрытия;
• расстояние, которое оставляется между балками;
• временная нагрузка;
• нагрузка от перегородок на перекрытие.

Чтобы упросить расчет данного примера, можно принять массу перекрытия за 60 кг/м², нагрузку на каждое перекрытие за 250 кг/м², нагрузки на перегородки 75 кг/м², а вес метра балки равным 18 кг. При расстоянии между балками в 60 см, коэффициент k будет равен 0,6.

Если подставить все эти значения в формулу, то получится:

q = ( 60 + 250 + 75 ) * 0,6 + 18 = 249 кг/м.

Для расчета изгибающего момента следует воспользоваться формулой f = (5 / 384) * [(qn * L4) / (E * J)] £ [¦].

Подставив в нее данные, получается f = (5 / 384) * [(qn * L4) / (E * J)] = (5 / 384) * [(249 * 44) / (100 000 * 10)] = 0,13020833 * [(249 * 256) / (100 000 * 10)] = 0,13020833 * (6 3744 / 10 000 000) = 0,13020833 * 0,0000063744 = 0,00083 м = 0,83 см.

Именно это и является показателем прогиба при воздействии на балку максимальной нагрузки. Данные расчеты показывают, что при действии на нее максимальной нагрузки, она прогнется на 0,83 см. Если данный показатель меньше 1, то ее использование при указанных нагрузках допускается.

Использование таких вычислений является универсальным способом вычисления жесткости конструкции и величины их прогибания. Самостоятельно вычислить данные величины достаточно легко. Достаточно знать необходимые формулы, а также высчитать величины. Некоторые данные необходимо взять в таблице. При проведении вычислений крайне важно уделять внимание единицам измерения. Если в формуле величина стоит в метрах, то ее нужно перевести в такой вид. Такие простые ошибки могут сделать расчеты бесполезными. Для вычисления жесткости и максимального прогиба балки достаточно знать основные характеристики и размеры материала. Эти данные следует подставить в несколько простых формул.

Расчет балки

построение эпюр в балках

Расчетная схема № 402112

Почему не бесплатно? — Сайт создан исключительно на энтузиазме автора и дабы этот энтузиазм не угас, хотелось бы его подкрепить хоть каким-нибудь материальным поощрением. Кроме того, возросшее количество пользователей вынудило перейти на платный хостинг.

Условия оплаты? — Взнос денег считаем спонсорским взносом, поэтому ни о каком возврате речь идти не может, тем более суммы мизерные — практически не о чем спорить.
Но! Если Вы оплатили взнос, но недовольны результатом, Вы всегда можете обратиться за помощью к автору — Telegram: sopromat_xyz WhatsApp

А Ваш сайт не сворует мой номер карты, пароли и т.д. — Это невозможно! После того, как Вы нажмете «Перевести», Вы будете направлены на страницу Яндекса (можете проверить в адресной строке), и все дальнейшие операции будете производить на сервисе Яндекса, так что со стороны сайта Вам ничего не грозит.

Жесткая заделка

Шарнирная опора

Врезной шарнир

Сосредоточенная сила F

Сосредоточенный момент M

Распределенная нагрузка

Подбор сечения и прогибы

подобрать двутавр [σ] = МПа

подобрать круг [σ] = МПа

подобрать квадратное сечение [σ] = МПа

подобрать трубчатое сечение [σ] = МПа при d/D=

подобрать прямоугольное сечение [σ] = МПа при h/b=

записать уравнения начальных параметров для каждого участка и посчитать прогибы и углы поворота в промежуточных точках

Расчет статически неопределимой балки

Поскольку данная балка является статически неопределимой, для нее нельзя определить внутренние усилия и реакции опор только методами статики (с помощью уравнений равновесия).

Как правило, для таких случаев сначала следует раскрыть статическую неопределимость, используя один из методов:

• метод сил
• метод уравнения трех моментов
• метод интегрирования дифференциального уравнения изгиба

При раскрытии статической неопределимости определяются некоторые параметры (реакции опор либо опорные моменты), имея которые дальнейший расчет уже возможен с помощью уравнений равновесия.

Будем считать, что статическая неопределимость раскрыта и эпюры уже построены

Степень статической неопределимости для данной балки равна

где m = — количество связей, s = — к-во шарниров.

Записываем уравнения поперечных сил и изгибающих моментов на участках балки , используя метод сечений

На участке AB: (0 ≤ z₁ ≤ 2 м )

На участке BC: (2 ≤ z₂ ≤ 3 м )

M(z₂) = + R_A · z — P·(z — 2) — q₁·(z — 2) 2 /2 = + 2.889 · z — 12·(z — 2) — 6·(z — 2) 2 /2

На участке CD: (3 ≤ z₃ ≤ 4 м )

M(z₃) = + R_A · z + R_C · (z — 3) — P·(z — 2) — q₁·(z — 2) 2 /2 = + 2.889 · z + 23.56 · (z — 3) — 12·(z — 2) — 6·(z — 2) 2 /2

На участке DE: (4 ≤ z₄ ≤ 4.5 м )

Q(z₄) = + R_A + R_C — P — Q₁ = + 2.889 + 23.56 — 12 — 12 = 2.444 кН

M(z₄) = + R_A · z + R_C · (z — 3) — P·(z — 2) — Q₁·(z — 3) = + 2.889 · z + 23.56 · (z — 3) — 12·(z — 2) — 12·(z — 3)

На участке EF: (4.5 ≤ z₅ ≤ 5 м )

Q(z₅) = + R_A + R_C — R_E — P — Q₁ = + 2.889 + 23.56 — 8 — 12 — 12 = -5.556 кН

M(z₅) = + R_A · z + R_C · (z — 3) — R_E · (z — 4.5) — P·(z — 2) — Q₁·(z — 3) = + 2.889 · z + 23.56 · (z — 3) — 8 · (z — 4.5) — 12·(z — 2) — 12·(z — 3)

На участке FK: (5 ≤ z₆ ≤ 6 м )

Q(z₆) = + R_A + R_C — R_E — P — Q₁ = + 2.889 + 23.56 — 8 — 12 — 12 = -5.556 кН

M(z₆) = + R_A · z + R_C · (z — 3) — R_E · (z — 4.5) — P·(z — 2) + M — Q₁·(z — 3) = + 2.889 · z + 23.56 · (z — 3) — 8 · (z — 4.5) — 12·(z — 2) + 8 — 12·(z — 3)

Максимальный момент в балке составляет M_max = 6.33 кНм. По этому значению подбираем сечение балки.

Условие прочности при изгибе σ = M_max / W ≤ [σ]

Отсюда, минимально необходимый момент сопротивления вычисляем по формуле W_min=M_max / [σ]

Подбираем двутавровое сечение при допускаемом напряжении [σ] = 160 МПа
W_min=6330 / 160 = 39.5625 см 3
Из сортамента выбираем двутавр №10 с моментом сопротивления W = 39.6 см 3 и площадью A = 12 см 2
Максимальные нормальные напряжения в двутавре составляют
σ_max = M_max/Wx = 6330/39.6 = 159.85 МПа
Максимальные касательные напряжения в двутавре (на центральной оси) составляют
τ_max = Q_max×Sx/b×Ix = 15100×20.43×10 -6 /0.0045×198×10 -8 = 34.623×10 6 Па = 34.623 МПа
Касательные напряжения на границе полки и стенки составляют
τ_max = Q_max×Sx’/b×Ix = 15100×18.37×10 -6 /0.0045×198×10 -8 = 31.132×10 6 Па = 31.132 МПа,
где статический момент отсеченной полки составляет
Sx’=b×t×(h-t)/2=5.5×0.72×(10-0.72)/2=18.37 см 3 .
Эпюры нормальных и касательных напряжений для двутавра:

Подбираем квадрат.
W_min=6330 / 160=40 см 3
Момент сопротивления квадратного сечения
W=a 3 /6
Сторона квадрата будет такой a= 6.2 см
Площадь сечения A=a 2 =6.2 2 =38.44 см 2

Записываем уравнения углов поворота и прогибов по методу начальных параметров

На участке AB: (0 ≤ z₁ ≤ 2 м )

На участке BC: (2 ≤ z₂ ≤ 3 м )

EJ×φ(z) = EJ×φ + R_A·z 2 /2 — P·(z — 2) 2 /2 — q₁·(z — 2) 3 /6

На участке CD: (3 ≤ z₃ ≤ 4 м )

EJ×φ(z) = EJ×φ + R_A·z 2 /2 + R_C·(z — 3) 2 /2 — P·(z — 2) 2 /2 — q₁·(z — 2) 3 /6

На участке DE: (4 ≤ z₄ ≤ 4.5 м )

EJ×φ(z) = EJ×φ + R_A·z 2 /2 + R_C·(z — 3) 2 /2 — P·(z — 2) 2 /2 — q₁·(z — 2) 3 /6 + q₁·(z — 4) 3 /6

На участке EF: (4.5 ≤ z₅ ≤ 5 м )

EJ×φ(z) = EJ×φ + R_A·z 2 /2 + R_C·(z — 3) 2 /2 — R_E·(z — 4.5) 2 /2 — P·(z — 2) 2 /2 — q₁·(z — 2) 3 /6 + q₁·(z — 4) 3 /6

EJ×v(z) = EJ×v + EJ×φ×z + R_A·z 3 /6 + R_C·(z — 3) 3 /6 — R_E·(z — 4.5) 3 /6 — P·(z — 2) 3 /6 — q₁·(z — 2) 4 /24 + q₁·(z — 4) 4 /24

На участке FK: (5 ≤ z₆ ≤ 6 м )

EJ×φ(z) = EJ×φ + R_A·z 2 /2 + R_C·(z — 3) 2 /2 — R_E·(z — 4.5) 2 /2 — P·(z — 2) 2 /2 + M· (z — 5) — q₁·(z — 2) 3 /6 + q₁·(z — 4) 3 /6

EJ×v(z) = EJ×v + EJ×φ×z + R_A·z 3 /6 + R_C·(z — 3) 3 /6 — R_E·(z — 4.5) 3 /6 — P·(z — 2) 3 /6 + M· (z — 5) 2 /2 — q₁·(z — 2) 4 /24 + q₁·(z — 4) 4 /24

Из условий закрепления по этим уравнениям вычислим начальные параметры:

— начальный угол поворота φ = -3.583 кНм 2

— начальный прогиб балки v = 0 кНм 3

Найдем углы поворота и прогибы сечений на каждом участке

Расчет балок из труб, круглого, квадратного, шестигранного и прямоугольного проката на изгиб и прогиб – калькулятор онлайн

Онлайн калькулятор для расчета на изгиб/прогиб

Предварительные соображения

Калькулятор предусматривает расчёт балок из некоторых видов проката на изгиб и прогиб для различных схем их крепления и нагрузки. Нагрузка балок может быть распределённой (“q” на схемах 3, 4, 5, 9, 15 и др.) или сосредоточенной (“P” на схемах 1, 2, 6, 7, 8 и др.)

Крепление балок может быть: а)консольным с жесткой заделкой одного из концов (например, схемы 1, 2, 3 и другие); б)”заделка – заделка”, когда оба конца балки жестко защемлены (заделаны), схемы 6, 7, 8, 9; в)”шарнир – шарнир” (схемы 12, 13, 14, 15 и другие), причём левый шарнир неподвижный а правый подвижный; г)”заделка – шарнир” (схемы 9, 10, 11 др.)

Жесткая заделка балки предотвращает поворот балки и перемещение её в любом направлении. Неподвижный шарнир допускает только поворот балки в месте крепления в вертикальной плоскости. Подвижный шарнир допускает поворот балки в месте крепления в вертикальной плоскостии и перемещение вдоль её собственной оси. Эти перемещения весьма незначительны и являются следствием деформации балки под нагрузкой.

Основным видом этой деформации является её прогиб, величина которого наряду с приложеной к балке нагрузкой зависит также от длины балки, размеров её поперечного сечения и физических характеристик материала, в данном случае от его модуля упругости (“E”). Модуль упругости углеродистой стали равен (2-2.1)*10^5 MПа; легировнной (2.1-2.2)*10^5 MПа; поэтому в калькуляторе принято среднее значение 2.1*10^5 MПа, что составляет 2142000кг.см2

Из размерных характеристик поперечного сечения балки для расчёта прогиба испльзуется момент инерции сечения (“I”); величина прогиба зависит также от положения проверяемой точки балки относительно опор. Допустимая величина прогиба балок определяется их назначением и местом в строительных кострукциях и реламентируется соответствующим СНиП; в легких случаях она не должна превышать 1/120 – 1/250 длины балки.

Поэтому настоятельно рекомендуется проверять результат расчета на допустимость.

Предназначение калькулятора для определения изгиба

Для создания каркасов различных строений самое большое распространение получила древесина. Из нее, как из пластилина, можно сотворить конструкцию любой сложности. Однако далеко не последнее место занимает и такой конструкционный материал как различные металлические профили.

Их выгодно отличает такое свойство как пластичность, долговечность и прочность. Не последнее место среди таких материалов занимают профильные и круглые трубы. Попытайтесь представить себе навес для автомобиля из профильной трубы с покрытием из поликарбоната и такое же строение из уголка.

Похоже, двух мнений быть не может. А любая балка из трубы в конструкции должна быть просчитана. Это необходимо по двум причинам:

• Получить объект с достаточным запасом прочности под воздействием собственного веса, а также ветровых и снеговых нагрузок.
• Подобрать минимально допустимый для строения профиль с целью минимизировать расходы на материалы.

Для достижения этой цели необходимо воспользоваться нашим онлайн калькулятором и рассчитать балку из трубы на изгиб. Это в случае, если деталь закреплена с одной стороны (консольная). Если же закреплены оба конца, понадобится рассчитать трубу на прогиб.

При этом необходимо учитывать следующие обстоятельства:

1. Размеры и сечение: (профильная или круглая). Для профильной прямоугольной трубы расчет производится с учетом направления воздействия. При расчете балок из квадратной трубы этот фактор одинаков для любого направления воздействия.
2. Прочностные характеристики материала с учетом толщины стенок и марки материала. Это особенно актуально при использовании балок из круглой трубы, расчет которой в значительной степени зависит от указанных характеристик ввиду многообразия применяемых материалов.

Виды вероятных нагрузок

Как можно классифицировать нагрузки на балку из трубы? В соответствии с СП 20.13330.2011 «Нагрузки и воздействия» моменты нагружения конструкции можно распределить по следующим признакам:

• постоянные – давление и вес которых не изменяются с течением времени, это такие, как собственный вес конструкции;
• временные длительные, учитывающие вес дополнительных конструкций сооружения, включая оборудование, мебель и прочее;
• кратковременные поперечные, зависящие от внешних условий эксплуатации – нагрузки от ветра, снега или дождя, для определения которых производится собственный расчет, зависящий от района расположения объекта. Такие нагружения в экстремальных условиях создают условия, при которых возможен прогиб балки из трубы.
• особые условия воздействия, к которым можно отнести воздействие от удара автомобиля во время парковки, в результате которого опора может прогибаться;
• сейсмические – для местностей с определенной сейсмической активностью.

Прочностью перекрытия определяется уровень безопасности проживания на загородном участке или в деревенском доме.

Степень нагружения конструкций можно подбирать по таблицам, при этом учитываются:

1. величина момента инерции, обозначенная в стандартах;
2. длина пролета;
3. величина нагрузки;
4. модуль Юнга (справочные данные).

В таблицах приводятся готовые данные, рассчитанные по специальной формуле например для круглых, квадратных и прямоугольных профилей. Все прочностные расчеты несущих конструкций по определению сложны в исполнении и требуют специальной инженерной подготовки в области сопротивления материалов. Поэтому лучше воспользоваться специальным онлайн-калькулятором. Чтобы рассчитать нагрузки достаточно ввести исходные данные в таблицу и на выходе можно получить точный результат быстро и без особых затруднений.

Балочная ферма, подсчет которой произведен таким образом, будет надежной конструкцией на долгое время. При правильном расчете предельная жесткость перекрытия гарантирована.

Предлагаем произвести ориентировочный расчет балок на прогиб и изгиб из круглого, квадратного, шестигранного и прямоугольного проката калькулятором.

Перед произведением расчетов настоятельно рекомендуем ознакомиться с расположенной ниже инструкцией

Расчет прогиба балки методом начальных параметров

Автор: Константин Вавилов · Опубликовано 23.10.2015 · Обновлено 15.05.2018

В этой статье будут рассмотрены основные нюансы расчета прогибов, методом начальных параметров, на примере консольной балки, работающей на изгиб. А также рассмотрим пример, где с помощью универсального уравнения, определим прогиб балки и угол поворота.

Теория по методу начальных параметров

Возьмем консольную балку, нагруженную сосредоточенной силой, моментом, а также распределенной нагрузкой. Таким образом, зададимся такой расчетной схемой, где присутствуют все виды нагрузок, тем самым, охватим всю теоретическую часть по максимуму. Обозначим опорные реакции в жесткой заделке, возникающие под действием внешней нагрузки:

Выбор базы и обозначение системы координат

Для балки выберем базу с левой стороны, от которой будем отсчитывать расстояния до приложения сил, моментов, начала и конца распределенной нагрузки. Базу обозначим буквой O и проведем через нее систему координат:

Базу традиционно выбирают с левого краю балки, но можно выбрать ее и справа. Тогда в уравнении будут противоположные знаки, это может пригодиться в некоторых случаях, упростит немного решение. Понимание, когда принимать базу слева или справа, придет с опытом решения задач на метод начальных параметров.

Универсальное уравнение прогибов для балки

После введения базы, системы координат и обозначении расстояний а, б, в, г записываем универсальную формулу, с помощью которой, будем рассчитывать прогиб балки (вертикальное перемещение сечения K, находящегося на свободном торце балки): Теперь поговорим об этой формуле, проанализируем так сказать:

• E – модуль упругости;
• I – момент инерции;
• V_k – прогиб сечения K;
• V_O – прогиб сечения O;
• θ_O – угол поворота сечения О.

Не буду приводить вывод этой формулы, не хочу отпугивать читателей, продвинутые студенты могут ознакомиться с выводом самостоятельно в учебнике по сопромату. Я только расскажу об основных закономерностях этого уравнения и как записать его для любой балки постоянного сечения.

Итак, изучаем эту формулу с лева направо. В левой части уравнения обознается искомый прогиб, в нашем случае V_k, который дополнительно умножается на жесткость балки — EI:В уравнении всегда учитывается прогиб сечения балки, совпадающего с нашей базой EIV_O:

Также всегда учитывается угол поворота сечения совпадающего с выбранной базой. Причем, произведение EIθ_O всегда умножается на расстояние от базы до сечения, прогиб которого рассчитывается, в нашем примере — это расстояние г.

Следующие компоненты этого уравнения учитывают всю нагрузку находящуюся слева от рассматриваемого сечения. В скобках расстояния от базы до сечения отнимаются расстояния от базы до соответствующей силы или момента, начала или конца распределенной нагрузки.

Скобка, в случае с сосредоточенными силами, возводится в 3 степень и делится на 6. Если сила смотрит вверх, то считаем ее положительной, если вниз, то в уравнении она записывается с минусом:

В случае с моментами, скоба возводится во 2 степень и делится на 2. Знак у момента будет положительный, когда он направлен почасовой стрелке и отрицательным, соответственно, когда против часовой стрелки.

Учет распределенной нагрузки

Теперь поговорим о распределенной нагрузке. Как уже говорилось, в уравнении метода начальных параметров должно учитываться начало и конец распределенной нагрузки, но конец ее совпадает с сечением, прогиб которого мы хотим вычислить, поэтому в уравнение попадает только ее начало.

Причем важно, даже если бы в этом сечении была бы сила или момент, их бы так же не учитывали. Нас интересует все, что находится слева от рассматриваемого сечения.

Для распределенной нагрузки скобочка возводится в 4 степень и делится на 24. Правило знаков такое же, как и для сосредоточенных сил:

Граничные условия

Чтобы решить уравнение нам понадобятся еще кое-какие данные. С первого взгляда в уравнении у нас наблюдается три неизвестных: V_K, V O и θ_O. Но кое-что мы можем почерпнуть из самой схемы. Мы знаем, в жесткой заделке не может быть никаких прогибов, и ни каких поворотов, то есть V_O=0 и θ_O=0, это и есть так называемые начальные параметры или их еще называют граничными условиями. Теперь, если бы у нас была реальная задача, мы бы подставили все численные данные и нашли перемещение сечения K.

Если бы балка была закреплена с помощью шарнирно подвижной и неподвижной опоры, тогда мы бы приняли прогибы в опорах равными нулю, но угол поворота в опорах был бы уже отличен от нуля. Более подробно об этом рассказано в другой моей статье, посвященной методу начальных параметров на примере балки на двух опорах .

Чуть не забыл про еще одну величину, которую часто требуется определять методом начальных параметров. Как известно, при изгибе, поперечные сечения балок помимо того, что перемещаются вертикально (прогибаются) так еще и поворачиваются на какой-то угол. Углы поворота и прогибы поперечных сечений связаны дифференциальной зависимостью.

Если продифференцировать уравнение, которое мы получили для прогиба поперечного сечения K, то получим уравнение угла поворота этого сечения:

Пример расчета прогиба балки

Для закрепления пройденного материала, предлагаю рассмотреть пример с заданными численными значениями всех параметров балки и нагрузок. Возьмем также консольную балку, которая жестко закреплена с правого торца. Будем считать, что балка изготовлена из стали (модуль упругости E = 2·10 5 МПа), в сечении у нее двутавр №16 (момент инерции по сортаменту I = 873 см 4 ). Рассчитывать будем прогиб свободного торца, находящегося слева.

Подготовительный этап

Проводим подготовительные действия, перед расчетом прогиба: помечаем базу O, с левого торца балки, проводим координатные оси и показываем реакции, возникающие в заделке, под действием заданной нагрузки:

В методе начальных параметров, есть еще одна особенность, которая касается распределенной нагрузки. Если на балку действует распределенная нагрузка, то ее конец, обязательно должен находиться на краю балки (в точке наиболее удаленной от заданной базы). Только в таком случае, рассматриваемый метод будет работать. В нашем примере, нагрузка, как видно, начинается на расстоянии 2 м. от базы и заканчивается на 4 м. В таком случае, нагрузка продлевается до конца балки, а искусственное продление компенсируется дополнительной, противоположно-направленной нагрузкой. Тем самым, в расчете прогибов будет уже учитываться 2 распределенные нагрузки:

Расчет прогиба

Записываем граничные условия для заданной расчетной схемы:

V_A = 0 при x = 6м

θ_A = 0 при x = 6м

Напомню, что нас, в этом примере, интересует прогиб сечения O (V_O). Для его нахождения составим уравнение, для сечения A, в которое будет входить искомая величина:

В полученном уравнении, у нас содержится две неизвестные величины: искомый прогиб V_O и угол поворота этого сечения — θ_O:

Таким образом, чтобы решить поставленную задачу, составим дополнительное уравнение, но только теперь, не прогибов, а углов поворотов, для сечения A:Из второго уравнения, найдем угол поворота:После чего, рассчитываем искомый прогиб:

Таким образом, свободный торец такой балки, прогнется практически на 6 см. Данную задачу, можно решить несколько проще, если ввести базу с правого торца. В таком случае, для решения потребовалось бы лишь одно уравнение, однако, оно было бы немного объемнее, т.к. включало реакции в заделке.